Voltage Control
Applets
significance of voltage control
Typical ranges of quantities
active power P = (-100% ...) 0% ... +100%
reactive power Q = -100% ... + 100%
current I = 0% ... 100% Ir (rated or nominal value)
voltage U = ?
why not U = 0 ... 100% in 400 V (low voltage) level ?
house hold consumers, equipment 95% ... 105%
=> LV U = 95% ... 105% (acording to country specific standards)
why not 500 kV in 400 kV voltage level ?
insulation of lines and cabels, switches
insulation and saturation of transformers
why not 300 kV in 400 kV voltage level ?
consider: PLoad = 3 U I , QLoad = 0
I = PLoad / 3 U
I high for low U
reduced transmission capacity
increased losses
PLoss = R | I | ^2
=> EHV, HV U = 90% ... 110%
causes of low voltages
source voltage
generator terminal voltage
transformer ratio / tap setting
voltage drop
line length, load current
S = 3 U * I*
I = ( P - j Q ) / 3 UL*
US = UL + ( R + j X ) * I
US = UL + ( R + j X ) * ( P - j Q ) / 3 UL*
for UL = UL + j 0
US = UL + ( R P + X Q + j ( X P - R Q ) ) / 3 UL
real part: aprox. = absolute value = voltage magnitude
imaginary part (small, phase angle between US and UL)
for HV and EHV R << X (~10%)
voltage magnitude mainly governed by Q
phase angle mainly governed by P
(remember dU/dQ >> dU/dP for transmission lines)
means of voltage control
- transformer taps
- injection of reactive power
- shunt capacitors
- shunt reactors, compensation coils
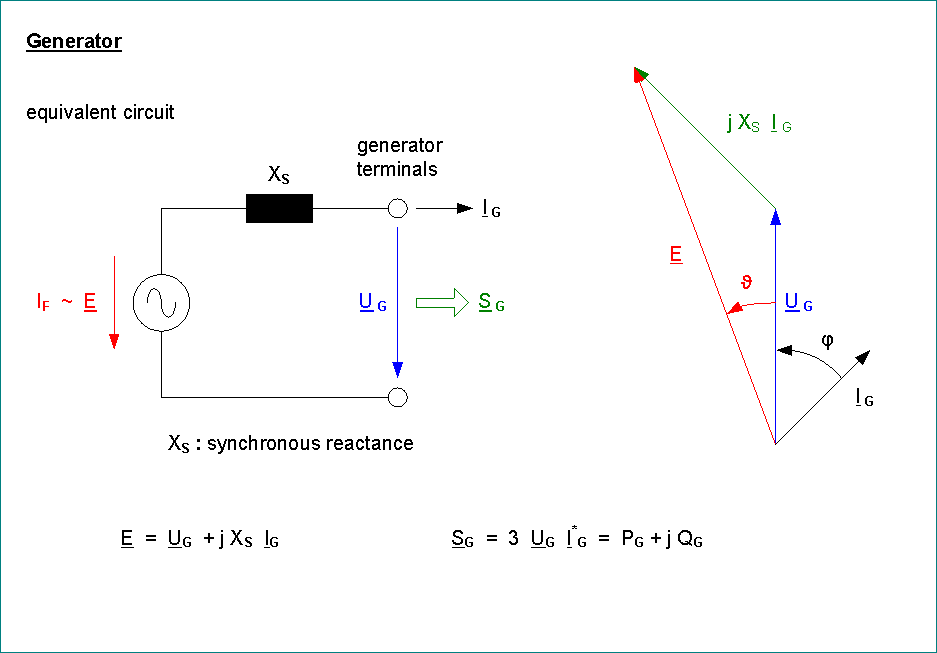
- generator, excitation system, P > 0, Q < 0 or Q > 0, generator terminal voltage
- phase shifters, synchronous condensors, P = 0, Q > 0 or Q < 0
- static var compensation, semiconductor controlled capacitors and reactors
- series compensation of long transmission lines
- (DC transmission)

load flow calculations
Free load flow demo: Power World Simulator
given:
P, Q for all load buses
P, Q or P, U for generator buses / power injections"
data of lines and transformers
find:
U, <) for all buses
I, P, Q for all branches
Q for P,U generators
active and reactive power losses
single branch
total netzwork
load flow equations => nonlinear set of equations ( 2 x number of buses)
Newton-Raphson-method

